giroscopio

El giroscopio es un dispositivo mecánico formado esencialmente por un cuerpo con simetría de rotación que gira alrededor de su eje de simetría. Cuando se somete el giroscopio a un momento de fuerza que tiende a cambiar la orientación del eje de rotación su comportamiento es aparentemente paradójico ya que el eje de rotación, en lugar de cambiar de dirección como lo haría un cuerpo que no girase, cambia de orientación en una dirección perpendicular a la dirección "intuitiva".
El giroscopio fue inventado en 1852 por Léon Foucault, quien también le dio el nombre, montando una masa rotatoria en un soporte de Cardano para un experimento de demostración de la rotación de la tierra. La rotación ya había sido demostrada con el péndulo de Foucault. Sin embargo no comprendía el por qué la velocidad de rotación del péndulo era más lenta que la velocidad de rotación de la tierra por un factor , donde representa la latitud en que se localiza el péndulo. Se necesitaba otro aparato para demostrar la rotación de la tierra de forma más simple. Foucault presentó así un aparato capaz de conservar una rotación suficientemente rápida (150 a 200 vueltas por minuto) durante un tiempo suficiente (una decena de minutos) para que se pudiesen hacer medidas. Esta proeza mecánica (para la época) ilustra el talento de Foucault y su colaborador Froment en mecánica.
Foucault también se dio cuenta de que su aparato podía servir para indicar el Norte. En efecto, si se impiden ciertos movimientos del soporte del giroscopio, este se alinea con el meridiano. Esto permitió la invención del girocompás.
Los giroscopios se han utilizado en girocompases y giropilotos. Los giroscopios también se han utilizado para disminuir el balanceo de navíos, para estabilizar plataformas de tiro y para estabilizar plataformas inerciales sobre las cuales están fijados captadores de aceleración para la navegación inercial en aviones y misiles construidos antes de la aparición del GPS. El efecto giroscópico es la base del funcionamiento de los juguetes trompo o peonza y dynabee.

[editar] El efecto giroscópico

Cuando se empuja el lado derecho hacia abajo, este, en lugar de bajar, se mueve hacia el observador.

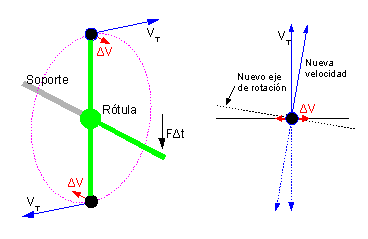
Cuando se da un golpecito en la extremidad de la barra horizontal se comunica a las masas una velocidad horizontal perpendicular a sus velocidades tangenciales.

Vista desde arriba del dibujo de izquierda. Las velocidades de la masa de arriba están dibujadas en trazos continuos y las de la masa de abajo en punteado.

[editar] Descripción del efecto

Supongamos un giroscopio formado por un disco montado sobre un eje horizontal, alrededor del cual el disco gira libremente a gran velocidad, como se observa en la figura de la derecha. Un observador mantiene el eje del fondo con la mano izquierda y el eje de delante con la mano derecha. Si el observador trata de hacer girar el eje hacia la derecha (bajando la mano derecha y subiendo la mano izquierda) sentirá un comportamiento muy curioso, ya que el giroscopio empuja su mano derecha y tira de su mano izquierda. El observador acaba de sentir el efecto giroscopio. Es una sensación muy sorprendente porque da la impresión de que el giroscopio no se comporta como un objeto "normal".

[editar] Explicación del efecto

Sea el objeto dibujado en la imagen de la derecha, formado por dos masas (en negro) de pequeñas dimensiones sujetas por una barra (en verde) en forma de T de masa despreciable y total rigidez. El centro de la T está fijado a un soporte por medio de una rótula que permite que la barra en T gire libremente alrededor de cualquier eje.
Las masas giran rápidamente alrededor del punto fijo con una velocidad tangencial . En el momento cuando las masas pasan por la posición del dibujo se da un golpecito hacia abajo en la extremidad libre de la T. Ese golpecito es en realidad una fuerza aplicada durante un corto instante y se llama, en Física, un impulso. La barra verde transmite ese impulso a las dos masas y le da a cada una, una pequeña velocidad horizontal 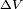perpendicular a la velocidad actual. Hacia la derecha en la masa de arriba y hacia la izquierda en la masa de abajo.
En el dibujo de la derecha aparecen las dos masas vistas desde arriba. Las velocidades comunicadas por la impulsión se suman a las velocidades corrientes. El resultado es que la velocidad de la masa de arriba se desvía ligeramente hacia la derecha y la velocidad de la masa de abajo se desvía hacia la izquierda. Y el resultado final es que el plano de rotación de las dos masas ha girado un poco hacia la derecha. O, dicho de otra manera, el eje de rotación de las dos masas ha girado hacia la derecha.
En un giroscopio no se trata de dos masas puntuales sino de masas distribuidas sobre todo el disco o el cilindro, pero eso no cambia el fondo de la explicación. Y cuando, en lugar de darle un impulso a un giroscopio, se le aplica un momento, se puede considerar este momento como una sucesión de cortos impulsos. Cada una de ellos añade a las masas una ínfima velocidad perpendicular a sus velocidades. Eso hace que la velocidad cambie de dirección sin cambiar de módulo.

[editar] Movimientos del giroscopio

Precesión (azul), nutación (rojo) y rotación (verde).

De acuerdo con la mecánica del sólido rígido, además de la rotación alrededor de su eje de simetría, un giróscopo presenta en general dos movimientos principales: la precesión y la nutación. Este hecho se deduce directamente de las ecuaciones de Euler.

[editar] Precesión

Cuando se aplica un momento a un cuerpo en rotación cuyo momento angular es 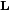, la dirección del eje de rotación del cuerpo se anima de un movimiento de rotación de velocidad angular . Esta velocidad angular, llamada velocidad de precesión, está relacionada con el momento y el momento angular por la fórmula:

La velocidad de precesión, como todas las velocidades angulares, se mide en radianes/segundo. En módulo, la velocidad de precesión es igual a . Es decir, para una misma cantidad de momento, la magnitud de la velocidad de precesión es tanto más pequeña cuanto el momento angular sea más grande. Y como el momento angular es el producto de la velocidad de rotación del giroscopio multiplicada por su momento de inercia, se puede reducir la velocidad de precesión aumentando el momento de inercia,la velocidad de rotación o ambas.
Aquí encontramos el interés de utilizar un giroscopio para conservar una referencia de dirección. Partiendo del reposo, todos los cuerpos conservan la orientación que tienen salvo cuando se les aplican momento externos. En ese caso, cuando un cuerpo no gira, el efecto del momento es el de crear una aceleración angular, la cual crea una velocidad angular creciente. Cuando el momento se interrumpe, el objeto sigue girando con la velocidad angular que adquirió. En cambio, cuando el mismo momento se aplica a un objeto en rotación, este comienza a girar con la velocidad de precesión calculada antes. Y cuando el momento se interrumpe, la precesión del objeto también se interrumpe. El resultado es que, en un giroscopio, los momentos parásitos tienen mucho menos efecto a largo plazo que en un objeto sin rotación. Además, se puede disminuir el efecto de esos momentos, aumentando el momento de inercia y la velocidad de rotación del giroscopio.

[editar] Nutación

Cuando el momento que causa la precesión cambia de valor, la velocidad de precesión también cambia de valor. Pero ese cambio no sucede instantáneamente. Hay un periodo de transición durante el cual el giroscopio "cede" un poquito al momento en la misma dirección que un objeto que no gira. Después el giroscopio recobra lo que había cedido, oscilando en la dirección del momento alrededor de la trayectoria de precesión final.
Este movimiento de oscilación transitorio se llama nutación.
Si el cambio de valor de los momentos se prolonga, la nutación puede durar mucho. Es el caso de la tierra. La atracción de la luna y del sol sobre el hinchamiento de la tierra en el ecuador es diferente entre el lado próximo y el lado lejano respecto al astro. Esa diferencia de atracción crea un momento, el cual causa la precesión de los equinoccios. Pero, como ni el sol ni la luna están en el plano del ecuador terrestre, el momento producido por estos astros cambia periódicamente y el movimiento de nutación de la tierra no se amortigua.

[editar] Bicicleta

Se ha supuesto durante mucho tiempo sobre que el efecto giroscópico estaba relacionado con el equilibrio de las bicicletas y motocicletas, aunque ha sido varias veces refutado¹ La forma más sencilla de comprobar que el efecto giroscópico no aporta estabilidad a una bicicleta es compensarlo con giróscopos en las ruedas. El experimento ha sido realizado² y se ha comprobado que la bicicleta es perfectamente estable sin efecto giroscópico neto. Sin embargo, es imposible conducir una bicicleta con el manillar bloqueado, lo que demuestra que son las fuerzas centrífugas (en el sistema de referencia de la bicicleta) que aparecen al mover el manillar las que le confieren estabilidad. Una bicicleta o una motocicleta lanzadas en movimiento sin conductor, siguen avanzando sin caerse hasta que encuentren un obstáculo o que pierdan su impulso. La trayectoria será una espiral, un círculo o, raramente, una recta.

Cuando la bicicleta se inclina hacia la izquierda, el momento creado por el peso sobre la rueda delantera desplaza el momento angular de esta hacia atrás y la hace virar hacia la izquierda. Esta situación continúa hasta que el momento creado por la fuerza centrífuga debida al giro compense el momento creado por el peso.

En el dibujo está representada una bicicleta en movimiento con el manillar derecho e inclinada un poco hacia la izquierda. El peso de la bicicleta crea un momento que tiende a inclinar aún más la bicicleta y a hacerla caer. Pero como la bicicleta avanza, la rueda de delante tiene un momento angular 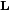dirigido hacia la izquierda. La rueda de atrás también tiene un momento angular, pero la manera en la cual está sujeta no le permite tener efecto en el equilibrio de la bicicleta. Este momento crea una variación , dirigida hacia atrás, del momento angular de la rueda de delante. Esto quiere decir que la rueda de delante gira hacia la izquierda, como si se hubiese girado el manubrio hacia la izquierda. La bicicleta comienza a voltear hacia la izquierda. Mientras el momento haga inclinarse más la bicicleta, el momento angular de la rueda de delante se inclinará hacia atrás, el manubrio hacia la izquierda y el radio de la trayectoria de la bicicleta disminuirá.
Visto desde el sistema acelerado y no inercial de la bicicleta, el radio de rotación disminuye lo cual aumenta la fuerza centrífuga. Esta fuerza centrífuga crea un momento que tiende a enderezar la bicicleta y a compensar el momento del peso que tiende a hacerla caer. Cuando los dos momentos terminan por compensarse, la bicicleta deja de inclinarse y el manubrio de girar hacia la izquierda. La bicicleta continúa en su trayectoria circular con radio constante. Si el frotamiento con el aire u otras cosas disminuyen la velocidad de la bicicleta, la fuerza centrífuga disminuirá, la bicicleta recomenzará a caerse lo cual hará girar el manubrio hacia la izquierda. El radio de giro disminuirá, lo cual aumentará la fuerza centrífuga hasta que ésta compense de nuevo el momento del peso. Cuando el manubrio llega a 90° o se bloquea, la bicicleta se cae.
Si se lanza una bicicleta con el manubrio inmovilizado (amarrado), la bicicleta se caerá como si estuviese parada.